A vector is a mathematical entity which consists in a series of numbers grouped together to represent another entity. Often, vectors are associated with spatial operations: the entities they represent can be either a point, or a direction. In computer science, vectors are used to represent entities known as features, measurable properties of an object (for instance, a human can be said to have features such as age, height, skin pigmentation, credit score and political leaning). Today, such representations are at the core of contemporary machine learning models, allowing a new kind of translation between the world and the computer.
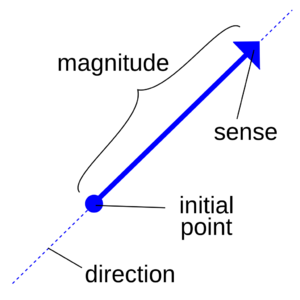
This essay sketches out some of the implications of using vectors as a way to represent non-computational entities in computational terms, like other visual mnemotechnics did in the past, by suggesting epistemological consequences in choosing a particular syntactic system over another. On one side, binary encoding allows a translation between physical phenomena and concepts, between electricity and numbers, enabling the implementation of symbolic logic in a formal and mechanical way (highlighting that truth really only is nothing more than a mathematical concept). On the other side, vectors suggest new perspectives on at least two levels: their relativity in storing (encoding) content and their locality in retrieving (decoding) content.
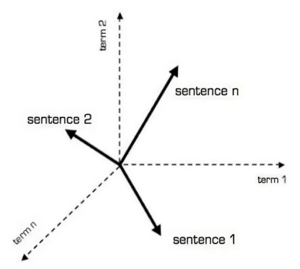
In machine learning, a vector represents the current values of the property of a given object, e.g. a human would have a value of 0 for the property "melting point", while water would have a value of non-0 for the property "melting point".
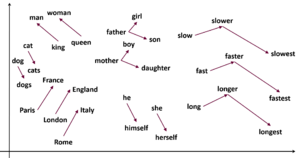
Vectors are thus always containing the potential features of the whole space in which they exist, and are more or less relatively tightly defined in terms of each other (as opposed to, say, alphabetical or cardinal ordering). The proximity, or distance, of vectors to each other is therefore essential to how we can use them to make sense. The meaning is therefore no longer created through logical combinations, but by spatial proximity in a specific semantic space. Truth moves from (binary) exactitude to (vector) approximation.
As we retrieve information stored in vectors, we therefore navigate semantic spaces. However, such a retrieval of information is only useful if it is meaningful to us; and in order to be meaningful, it navigates across vectors that are in close proximity to each other, focusing on re-configurable, (hyper-)local coherence to suggest meaningful structuring of content.

Given those the existence of features in relation to one another, and the construction of meaning through the proximity of vectors, we can see how semantic space is both malleable in storing meaning, structural in retrieving meaning, prompting questions of literacy. A next interesting inquiry is to think about the process through which this semantic space is being shaped, through the process of corporate training, and, in turn, shape us into specific communities of perceiving.